Многоступенчатая схема - отчаянная попытка увеличить соотношение масс ракеты для повышения delta V до значения, требуемого для выполнения задания. Для ракеты из одной ступени крайне сложно получить соотношение масс выше 15, и практически невозможно перейти за 20. До какого-то момента можно избавляться от структурной массы, но потом такая потеря в прочности приведёт к тому, что ускорение вырвет крепления и раздавит топливные баки как пустые жестянки. Без многоступенчатой схемы придётся также строить очень большие ракеты, из-за проблемы "минимального размера". Джерри Пурнелл написал: "Учтите, что для высокого соотношения масс вам нужна БОЛЬШАЯ ракета. Вы не можете сделать определённые части любой ракеты меньше некоторого предела. Это явление называется "минимальный предел размера" и означает, что кое-что просто нельзя сделать тоньше или легче. Камера сгорания должна выдерживать температуру. Трубы должны выдерживать давление. То, что ваша ракета меньше, ещё не означает, что температура или давление в трубах станут пропорционально меньше. Они останутся такими же." Пурнелл также заметил, что многоступенчатые ракеты заставляют разработчиков подсознательно воспринимать ракету не как некий летательный аппарат, а скорее как экзотический боеприпас из большого количества расходных частей. Расходных частей вместо частей многократного использования.

Многоступенчатая схема позволяет увеличить общее соотношение масс ракеты за 15, при том, что для отдельной ступени ракеты соотношение всё ещё меньше этого значения. Когда текущая ступень израсходует свою реакционную массу, она сбрасывается. Это избавляет нас от мёртвого груза её двигателей, топливных баков и структурных элементов. По сути, первая ступень - это ракета с полезной нагрузкой в виде остальных ступеней.

Вы обычно можете столкнуться с многоступенчатой схемой в экстремальных обстоятельствах, когда нужно разогнать значительное количество полезной нагрузки при взлёте с Терры на орбиту с помощью анемичных ракет на химическом топливе, (хотя в книге Joan Vinge THE OUTCASTS OF HEAVEN BELT Защитный Флот использовал скоростные корабли с высоким значением Delta V. Между планетами летали настоящие флотилии многоступенчатых космических аппаратов. ). Вам не потребуется многоступенчатая схема, если вы пользуетесь атомной ракетой. Ступени вряд ли нужны и в глубоком космосе, где всегда можно пользоваться двигателями с высокой скоростью истечения (и высоким удельным импульсом) что, к сожалению, также влияет на соотношение тяги к весу. Скорей всего, оно будет меньше единицы а потому эта система не может использоваться для взлёта с планеты - что в большинстве случаев является единственным недостатком. Это, в сущности, неплохо. Какой уважающий себя ракетчик захочет лететь на рассыпающемся на части китайском фейерверке, когда можно использовать более спокойные виды транспорта? Это не говоря о том, что ступени - не самый дешёвый расходный материал. Кроме того, увеличивается количество элементов, которые могут поставить миссию под угрозу, если выйдут из строя. В теории, можно избавляться от пустых топливных баков и двигателей поштучно. В действительности обычно сбрасывают пакет разгонников. Именно так взлетает космический челнок, на пачке твердотопливных разгонников, именно так должен был взлетать Otrag. Этот метод называют "параллельными ступенями". Многоступенчатая химическая ракета зачастую обладает разной скоростью истечения для отдельных ступеней. Это вызвано сложной оптимизацией, которую я лишь вкратце описал ниже (поскольку сам толком не понимаю). Тем не менее, я понял, что оптимизация в основном имеет отношение к взлёту, а не к перемещениям в космосе

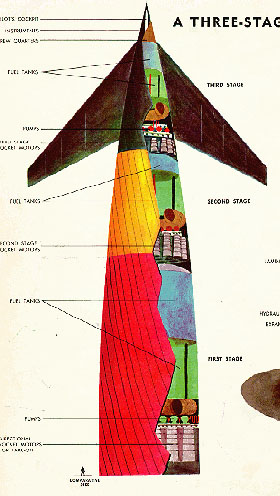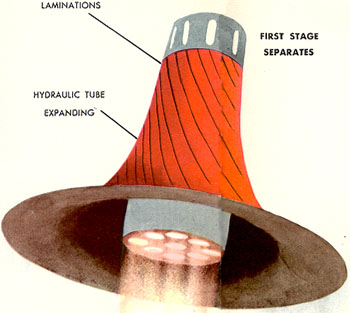Художник Earl Oliver Hurst. Диагональные линии - фрагмент системы безопасного спуска ступени. Её корпус формируют параллельные металлические полосы. После сброса, эти полосы с помощью гидравлической системы раскрываются во что-то вроде большого металлического тромбона. Это формирует жёсткий парашют, и позволяет надеяться на то, что после удара о землю ступень уцелеет для повторного использования.

Из книги The Outcasts of Heaven Belt автор Joan Vinge (1978):

С помощью многоступенчатой схемы можно увеличить эффективное соотношение масс для всей ракеты. Результаты для каждой ступени умножаются. В этом и заключается основная причина популярности многоступенчатой схемы, несмотря на все её недостатки.

При вычислении delta V отдельной ступени, вы пользуетесь стандартным уравнением delta V , но при вычислении соотношения масс вы используете общую массу всей ракеты за вычетом уже сброшенных ступеней.

Упрощённый пример: Возьмём Звёздное Копьё Тома Свифта. Масса в 100 тонн и три ступени. У каждой ступени химический двигатель. Скорость истечения составляет 4,500 м/с (я просто обожаю его удивительный солнечный ускоритель). Вспоминаем уравнение соотношения масс: R = (Mpt / Me) + 1 где R = соотношение масс (число) Mpt = масса реактивной массы (кг) Me = сухая масса ракеты (кг) Допустим, 80% массы Звёздного Копья составляет горючее первой ступени (Очевидно, что при массе корабля 100 тонн, это даст нам Mpt = 80 тонн), 10% отдадим на сухую массу первой ступени, а ещё 10% на массу остальной ракеты (что даст Me = 10 + 10 = 20 тонн).

Подставляем это в уравнение, и получем для первой ступени Звёздного Копья следующее: R = (Mpt / Me) + 1 R = (80 / 20) + 1 R = 4 + 1 R = 5 Это значит, что delta V первой ступени составит: Δv = Ve * ln[R] Δv = 4,500 * ln[5] Δv = 4,500 * 1.61 Δv = 7250 м/с Допустим, что две последующие ступени обладают теми же пропорциями (что на самом деле полный бред, но как пример - сойдёт). Общее delta V всех трёх ступеней: Δv = 3 * 4,500 * ln[5] Δv = 3 * 4,500 * 1.61 Δv = 3 * 7250 Δv = 21,800 m/s

Помните, эффективное соотношение масс вычисляется из перемножения индивидуальных соотношений масс каждой ступени. Таким образом, Звёздное Копьё получает соотношение масс как у одноступенчатой ракеты с 5 * 5 * 5 = 125! Похоже на истину? Давайте проверим:

Ну, 127 достаточно близко к 125, поскольку в данном случае нам важна сама идея.

Разумеется, поскольку только 10% каждой ступени составляет груз, реальная грузоподъёмность последней ступени 10% * 10% * 10% = 0.1%, и 0.1% от 100 тонн всего лишь 100 * 0.001 = 0.1 тонны, или 100 килограммов.

Общее значение delta V многоступенчатой ракеты, очевидно, сумма delta V каждой ступени. Поскольку delta V составляет Ve * ln[R], общее delta V трёхступенчатой ракеты составит: Δv = (Ve1 * ln[R1]) + (Ve2 * ln[R2]) + (Ve3 * ln[R3]) Где Δv = общее значение deltaV космического аппарата (м/с) Ve1 = Скорость истечения ступени 1 (м/с) Ve2 = Скорость истечения ступени 2 (м/с) Ve3 = Скорость истечения ступени 3 (м/с) R1 = Соотношение масс реактивной массы ступени 1 to к сухой массе ступени 1 и общей массе ступеней 2 и 3) R2 = Соотношение масс реактивной массы ступени 2 к сухой массе ступени 2 и общей массе ступени 3) R3 = Соотношение масс реактивной массы ступени 3 к сухой массе ступени 3

Пример: В ракетном клубе "Галилей" собрали трёхступенчатую ракету. Первая ступень имеет сухую массу 40 килограмм и 50 килограмм реактивной массы, с удельным импульсом 230 секунд (Скорость истечения составит 230 * 9.81 = 2260 м/с). Ступень два имеет сухую массу 22 килограмма, 15 килограмм горючего и удельный импульс 250 секунд (скорость истечения в 2450 м/с). Ступень три обладает сухой массой 12 килограмм и 9 килограммами топлива, с удельным импульсом 250 секунд (скорость истечения 2450 м/с). Полезная нагрузка ракеты 10 килограмм. Чему равно общее значение delta V? Вы наверное помните, что Соотношение Масс составляет: R = (Mpt / Me) + 1 Следовательно, для трёх ступеней, соотношение масс будет: R1= (50 / (40+22+15+12+9+10)) + 1 R1= (50 / 108) + 1 R1= 1.46 R2= (15 / (22+12+9+10)) + 1 R2= (15 / 53) + 1 R2= 1.28 R3= (9 / (12+10)) + 1 R3= (9 / 22) + 1 R3= 1.41

Общее Δ_v составит:

Художник Virgil Finlay

Ваша следующая забота - оптимальное соотношение масс каждой ступени. Я боялся этого вопроса. Ответ слегка затруднителен. У вас есть требования к Δv лётного задания Δvm, а также масса полезной нагрузки (погодный спутник, МКБР, командный и лунный модули программы Аполло, межпланетный военный корабль, орбитальный истребитель, ну или что-там-у-вас...). Для оптимизации многоступенчатой ракеты вы должны последовательно совершить описанные ниже действия. Они взяты из этого раздела. Вы крайне быстро поймёте на собственном опыте, почему это всё зовут "ракетной наукой." 1: ВЫБЕРИТЕ КОЛИЧЕСТВО СТУПЕНЕЙ 2: ОПРЕДЕЛИТЕ УДЕЛЬНЫЙ ИМПУЛЬС КАЖДОЙ СТУПЕНИ 3: ВЫБЕРИТЕ ПРОЦЕНТ ИНЕРТНОЙ МАССЫ ДЛЯ КАЖДОЙ СТУПЕНИ 4: ОПРЕДЕЛИТЕ ДОЛЮ Δv КАЖДОЙ СТУПЕНИ 5: ОПРЕДЕЛИТЕ РАЗМЕР СТУПЕНЕЙ И КОСМИЧЕСКОГО АППАРАТА 6: МИНИМИЗИРУЙТЕ МАССУ КОСМИЧЕСКОГО АППАРАТА ОПТИМИЗАЦИЕЙ ДОЛИ Δv КАЖДОЙ СТУПЕНИ

1: ВЫБЕРИТЕ КОЛИЧЕСТВО СТУПЕНЕЙ

Это мы обзовём n_stage. Выберите минимальное практичное количество ступеней. Посмотрите на возможные значения n_stage и сравните средние различия.

2: ОПРЕДЕЛИТЕ УДЕЛЬНЫЙ ИМПУЛЬС КАЖДОЙ СТУПЕНИ

Высокий удельный импульс - ваша главная забота. При взлёте также необходимо иметь соотношение тяги к весу выше 1.

Но иногда выгодно иметь реактивную массу высокой плотности (что ведёт к уменьшению удельного импульса). Иногда, если реактивная масса высокой плотности применяется в первых ступенях, это позволяет сэкономить на проценте инертной массы и облегчить мёртвый вес первой ступени. Но, только иногда. В других случаях это облегчит саму первую ступень, но увеличит общую массу вашего космического аппарата. Вам придётся проверять это самим.

3: ВЫБЕРИТЕ ПРОЦЕНТ ИНЕРТНОЙ МАССЫ ДЛЯ КАЖДОЙ СТУПЕНИ

Термин "инертная масса" обозначает массу ступени за вычетом топлива и полезной нагрузки. Общий термин "инертная масса" используется потому, что зная только массу груза, мы не имеем никаких способов более-менее точно разобраться с массой структурных элементов. Это забота инженеров после того, как им уже дали денег на разработку, а для наших целей сойдёт и так.

Для нахождения "процента инертной массы" мы делим инертную массу на общую массу ступени.

В существующих химических ракетах инертная масса ступени варьируется от 0.08 до 0.7.

4: ОПРЕДЕЛИТЕ ДОЛЮ Δ_v КАЖДОЙ СТУПЕНИ

Задача - так поделить между ступеними Δ_v, чтобы в итоге предельно снизить массу космического аппарата. Единственный способ это сделать - поиграть с доступными комбинациями (посмотрите на шаг 6 ниже).

В особых случаях, когда у ступеней одинаковое соотношение инертной массы и удельного импульса, у них также будет одинаковый процент Δ_v . Доля составит 1 / n_stage. Например, при четырёх ступенях, каждая даст 1/4 = 0.25 = 25% общего Δ_v.

5: ОПРЕДЕЛИТЕ РАЗМЕР СТУПЕНЕЙ И КОСМИЧЕСКОГО АППАРАТА

Начнём вычисления с последней (верхней) ступени, переходя затем к нижним. Нагрузка верхней ступени - реальная полезная нагрузка нашей ракеты. Нагрузка каждой нижестоящей ступени включает все верхние ступени плюс реальную полезную нагрузку.

Итак, начнём с верхней ступени. Масса её полезной нагрузки - вся наша реальная полезная нагрузка. Удельный импульс (I_sp) для этой ступени мы вычислили в шаге 2. Доля инертной массы (f_inert) вычислена в шаге 3. Ну и доля Δ_v (f_Δv) вычислена в шаге 4.

С этими значениями, мы вычисляем массу реактивной массы, инертную массу, а также изначальную массу нашей ступени.

Для вычисления массы реактивной массы: Удельный Импульс даёт нам Скорость Истечения:

Доля Δ_v и Δ_v нашего лётного задания дают Δ_v ступени:

Δ_vs и Скорость Истечения дадут нам Соотношение Масс:

масса полезной нагрузки, соотношение масс и доля инертной массы дадут нам массу реактивной массы:

Для вычисления инертной массы:

Наконец, для вычисления изначальной массы ступени:

Для следующей нижестоящей ступени и всех последующих за ней, используйте значение изначальной массы вышестоящей ступени M вместо массы полезной нагрузки M_pl, также используйте в формуле значения доли Δ_v удельный импульс и долю инертной массы для новой ступени. После этого просто подставляйте эти значения в уравнение выше.

Повторяйте, пока не закончите. Изначальная масса M последней ступени будет общей массой вашего космического аппарата. Смысл в том, чтобы сделать её минимальной возможной для поставленного задания.

6: МИНИМИЗИРУЙТЕ МАССУ КОСМИЧЕСКОГО АППАРАТА ОПТИМИЗАЦИЕЙ ДОЛИ Δ_v КАЖДОЙ СТУПЕНИ

Доля Δ_v каждой ступени должна различаться, чтобы подобрать идеальную комбинацию для уменьшения взлётной массы. Это достигается проведением сравнительного анализа доступных вариаций. Что значит, что компьютерной программе, гуманоидной кошке-рабыне или непосредственно вам придётся повторять шаги 4 и 5 в различных комбинациях Δ_v, пока вы не отыщите наиболее подходящее решение.

С двухступенчатой ракетой это, ну, я бы не стал говорить "легко", но всё же заметно проще чем расчёт для трёхступенчатой ракеты или космического аппарата из ещё большего количества ступеней. Для схемы из двух ступеней очевидно, что как только вы определили процент Δ_v для одной ступени, вы автоматически подобрали удачное решение для второй ступени (разумеется, это будет 1.0 - f_Δv1).

Итак, вы берёте спектр значения доли Δ_v первой ступени, допустим, от 0.2 до 0.8, и пересчитываете значение шаг за шагом, допустим, по 0.1 за шаг. Вычтите эти значения из 1.0 для вычисления доли второй ступени. Подставьте результаты в россыпь уравнений наверху, и у вас получится что-то вроде такого симпатичного графика:

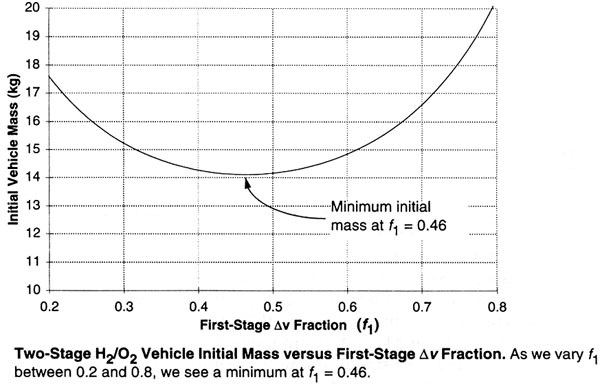
На графике вы сможете отыскать минимальное значение инертной массы космического аппарата и соответствующие доли Δ_v Такая вот оптимизация.

То же самое для трёх и более ступеней вызовет у вас изрядную боль где-то в gluteus maximus.

Нам требуется поиграть с двумя значениями Δ_v, чтобы найти эффективный минимум. Для трёхступенчатой системы мы повторям нарисованное выше для спектра значений f_Δv2 с выбором минимального f_Δv1 для каждого f_Δv2 (помните, f_Δv3 = 1.0 - f_Δv1 - f_Δv2). Мы можем вычислить изначальную массу космического аппарата (с минимизированным значением f_Δv1) и выбрать f_Δv2 с минимумом изначальной массы.