
 |

Если у вас найдётся мощная двигательная система, можно игнорировать всю эту чушь с орбитой Хохмана. Но лучше бы обзавестись действительно мощным двигателем. Чем-то научно-фантастическим, способным разгоняться на 1 g долгие дни, с аномально высоким delta V, оставляя далеко позади все технологии "ближнего прицела". Движок, способный на полном ходу влететь прямиком в Закон Джона
Но его наличие не отменяет математику. Просто вам понадобятся иные уравнения.
(Термин "Факельный корабль" придумал Роберт Хайнлайн и упоминал в своих книгах - "Фермер в небе", "Время для звёзд", "Двойная Звезда" и "Лифт в небеса". Иногда его называли "Факел Ортеги". В наши дни принято считать, что факел - разновидность мощного ядерного двигателя, но Хайнлайн имел в виду полную конверсию массы в энергию. Самое близкое из прогнозируемых технологий - лучевой двигатель на антиматерии.)
Итак, к уравнениям. Сперва выясняем расстояние между двумя планетами, например, Марсом и Террой. "Вышестоящая" планета находится дальше от Солнца, "нижестоящая" ближе. Расстояние от Солнца до вышестоящей планеты обозначено как Ds а до нижестоящей - Di.
Очевидно, что максимальное расстояние между планетами случается когда одна находится с одной стороны от солнца, а другая - прямо напротив. Это расстояние составит Ds + Di. И разумеется, что минимум придётся на тот момент, когда они на одной линии по одну сторону от Солнца - Ds - Di. Средняя дистанция между планетами обычно составляет плюс-минус Ds.
Просто выберите дистанцию между максимумом и минимумом. Если вас интересует вычисление реального расстояния между планетами в конкретный момент времени - это без меня, я не обладаю нужной для объяснения квалификацией. Поищите в сети программу "orrery".
Орбита Хохмана вовлекает максимум транзитного времени при минимуме deltaV "Брахистохронная" (или циклоидная) орбита сводит к минимуму транзитное время при высоких требованиях к deltaV - вы непрерывно разгоняетесь половину пути, затем поворачиваете корабль двигателями в другую сторону и непрерывно тормозите другую половину пути (Аппараты с более слабой ходовой разгоняются до определённой скорости, отключают двигатель, разворачиваются и какое-то время летят свободно перед тем, как начать торможение). Брахистохронная орбита не только самая быстрая, она также не ограничена необходимостью выждать окно запуска, как это бывает с орбитой Хохмана. Взлёт доступен в любой момент.
Важно помнить, что при прочих равных торможение занимает ровно столько же времени, сколько и разгон. Если кому-то из вас доводилось играть в древнюю настольную игру Triplanetary или новую игру Voidstriker то вы могли запомнить цену ошибки. Пять ходов непрерывного разгона значительно увеличивали скорость корабля, но в итоге оказывалось, что цена торможения в те же пять ходов приводит к вылету корабля за край игрового поля или удар о Марс на такой скорости, что от корабля не останется ровным счётом ничего, кроме дымящейся воронки. Вот почему брахистохронная орбита вовлекает разгон только до половины пути, а всё остальное занимает снижение скорости ради сброса её до нуля в конечной точке.
При известном ускорении вашего корабля (чаще всего комфортным для экипажа считается g или 9.81 м/с2) уравнение для брахистохронной траектории выглядит следующим образом:
T = 2 * sqrt[ D/A ]
где
Тимоти Чартерс предложил следующее уравнение для слабых аппаратов, не способных на постоянную работу двигателя.
T = ((D - (A * t^2)) / (A * t)) + (2*t)
гдеЕсли вы знаете время перелёта и вам требуется вычислить ускорение, уравнение выглядит следующим образом:
A = (4 * D) / T2
Помните, что длительные периоды разгона более чем на 1 g негативно сказываются на здоровье экипажа.
Не путайтесь в том, что могли отыскать в учебниках. Уравнение брахистохрона может выглядеть как T = sqrt[ 2 * D/A ] вместо T = 2 * sqrt[ D/A ], поскольку в учебнике можно увидеть что-то вроде D = 0.5 * A * T^2. Это всё потому, что D в учебнике обычно относится к средней точке траектории а не общей дистанции.
Уравнение из учебника превратится из
D = 0.5 * A * t^2
в
D * 0.5 = 0.5 * A * t^2
Решение для t даст нам t = sqrt(D/A) где t - время до точки торможения. Поскольку затем уйдёт столько же времени на само торможение, общее время T будет вдвое больше T = 2 * sqrt( D/A ). Что, в общем-то, уже один раз написано выше.
Ну а теперь к тому, насколько откормленной должна быть наша ракета. Берём дистанцию и ускорение из уравнений выше и получаем следующее:
Транзитное DeltaV = 2 * sqrt[ D * A ]
гдеРакета также должна уравнять скорость с планетой в точке прибытия. Орбита Хохмана обычно уже включает в общее значение
Орбитальная Скорость = sqrt[ (G * M) / R ]
гдеЕсли речь идёт о полётах в солнечной системе, уравнение превратится в
Орбитальная Скорость = sqrt[1.33e20 / R ]
Вычислите орбитальную скорость планеты старта и прибытия, вычтите меньшее из большего, и у вас останется DeltaV совпадающей скорости
DeltaV совпадающей скорости = sqrt[1.33e20 / Di ] - sqrt[1.33e20 / Ds ]
На взлёт и посадку также требуется deltaV.
DeltaV взлёта = sqrt[ (G * Pm) / Pr ]
гдеОбщее значение deltaV таким образом:
DeltaV Общее = sqrt(DeltaV Взлётное2 + DeltaV Транзитное2) + sqrt(DeltaV совпадающей скорости2 + DeltaV Посадки2)
Небольшие вычисления покажут, что такие требования находятся далеко за пределами моей таблицы сколько-то реализуемых двигателей
Если хотите лёгких путей - посмотрите на Таблицу лётных заданий Джона Роджера.
Для грубых оценок воспользуйтесь моей
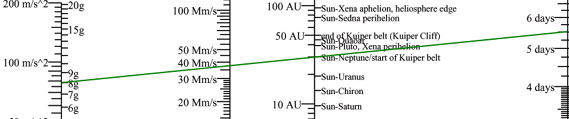
Номограммой транзитного времени.
Номограмма - устаревшее средство математических вычислений -
набор шкал на листе бумаги, используемых с помощью линейки или угольника. Не смотря на то, что он вдрызг устарел, у него есть огромное преимущество - наглядность. Распечатайте номограмму, возьмите линейку, и делайте по моему примеру
Постер 11" x 17" можно заказать тут:
 .
Стандартная отмазка: я её сделал, но не являюсь профессионалом и не гарантирую отсутствие ошибок.
.
Стандартная отмазка: я её сделал, но не являюсь профессионалом и не гарантирую отсутствие ошибок.
Допустим, наш космический аппарат обладает массой 1.5 килотонн (или 1500 метрических тонн). У него один газовый термальный ядерный двигатель (NTR-GAS MAX) и (совершенно безумное) соотношение масс 20. Уравнение для вычисления общего DeltaV Δv = Ve * ln[R]. На вашем карманном калькуляторе 98,000 * ln[20] = 98,000 * 2.9957 = 300,000 м/с = 300 км/с. В идеале это стоило бы загнать в транзитную номограмму, но в ней и так уже в глазах рябит от избыточной информации. Пользуйтесь этой.
Задача - перемещение на 0.4 AU (примерное расстояние от Солнца до Меркурия). Сколько времени займёт брахистохронная траектория с постоянным ускорением?

Изучаем номограмму. На шкале массы отмечаем 1.5 килотонн. На типе двигателя находим NTR-GAS MAX. Прикладываем угольник и находим пересечение с Ускорением. Получаем 2 метра в секунду за секунду (м/с^2).
Чтобы облегчить вашу жизнь, шкала ускорения также включает минимум взлётного значения для разных планет.
Итак, мы знаем максимальное ускорение 2 м/с^2 и максимум DeltaV в 300 км/с. Пока мы удерживаемся в этих пределах - всё прекрасно.

На шкале Ускорения отмечаем 2 м/с^2. На шкале Дистанции находим 0.4 AU. Прикладываем угольник и находим точку пересечения со шкалой Транзитного Времени. Получается чуть меньше четырёх дней.
Но подождите! Смотрите, куда ушло пересечение с общим значением DeltaV! Опаньки. Почти 750 км/с, а у нашего корабля в распоряжении лишь 300 км/с до полного израсходования горючего. Наш корабль не в состоянии воспользоваться этой траекторией.

Нюанс в том, что 2 м/с^2 - максимальное ускорение, никто не запрещает взять меньшее по расходу DeltaV значение. Вот чем хороша номограмма - виден спектр решений.
Угольник на отметку 0.4 AU и ведём его до пересечения с 300 км/с на шкале общего DeltaV. Ну вот, 0.4 м/с^2 и полётное время около недели. Поскольку это умещается в потребные нам рамки, корабль долетит без проблем (мы предполагаем, что система жизнеобеспечения достаточна для нужд экипажа в ходе этой недели).
Разумеется, если вам нужно располагать резервом по DeltaV в точке прибытия, можно придержать немного горючего. 250 км/с DeltaV, немного возни с линейкой и вы увидите, сколько уйдёт времени на сохранение резерва в 50 км/с в ваших топливных баках
Из книги есть скафандр - готов путешествовать Роберта Хайнлайна, 1958.
Что напомнило мне, что я так и не озаботился вычислением, сколько времени уйдёт на возвращение домой на одном же, если я вдруг не смогу настроить автоматическое пилотирование на восьми. Конечно, куда больше меня волновал побег из камеры, я даже не задумывался о том, что я буду делать если (поправка - когда) выберусь, но мог подумать о баллистике уже сейчас.
Книги мне не требовались. Я встречал людей, которые не способны отличить звезду от планеты и думают, что астрономические дистанции достаточно охарактеризовать как "большие". Ну, что-то вроде дикарского исчисления "один, два, три, много". Но хороший скаут знает основные факты, а такой помешанный на космосе как я - и кое-что ещё.
"Мама Варит Земляничный Морс А Юный Сын Уже Не Плачет". Не забудете, если повторите несколько раз? Тогда распишем подробно:
| Мама | МЕРКУРИЙ | $.39 |
| Варит | ВЕНЕРА | $.72 |
| Земляничный | ЗЕМЛЯ | $1.00 |
| Морс | МАРС | $1.50 |
| А | АСТЕРОИДЫ | (в ассортименте) |
| Юный | ЮПИТЕР | $5.20 |
| Сын | САТУРН | $9.50 |
| Уже | УРАН | $19.00 |
| Не | НЕПТУН | $30.00 |
| Плачет | ПЛУТОН | $39.50 |
(прим. переводчика: в оригинале "Mother very thoughtfully made a jelly sandwich under no protest." Литературный русский вариант взят из перевода Е. Беляевой А. Митюшкина, ЭКСМО, 2003)
"Цены" - расстояние от Солнца в астрономических единицах. Одна А.Е. - расстояние от Земли до Солнца, 93,000,000 миль. Это куда проще запомнить, чем безумные миллионы и миллиарды. А долларовые значки я использую потому, что шуршащие бумажки мне по вкусу. Папа считает это прискорбным, но надо же как-то запоминать, что у вас под носом.
Теперь к сути. По таблице от Плутона до Земли тридцать девять с половиной расстояний от Земли до Солнца. Однако, у Плутона и Меркурия орбиты сильно вытянуты. У Плутона расстояние до Солнца изменяется на два миллиарда миль, чокнуться можно. Больше, чем от Солнца до Урана. Плутон даже забирается внутрь орбиты Нептуна, а потом откатывается вдаль и маячит там пару столетий, совершая всего четыре оборота за тысячу лет.
Но в той статье говорилось, что на Плутоне начинается "лето". Значит, сейчас он находится вблизи орбиты Нептуна и будет находиться там до конца моей жизни - если бы я оставался в Кентервилле. Здесь же предсказать,сколько я проживу, трудновато. В общем, получилась круглая сумма - 30 Астрономических Единиц.
Задачки на ускорение проще пареной репы. s=1/2 at2; дистанция равна половине ускорения на квадрат времени. Если бы астрогация этим ограничивалась, любой новичок мог бы пилотировать корабль. Трудности происходят от гравитационных возмущений и всего, что движется одновременно в четырнадцати разных направлениях. Однако я мог пренебречь гравитационными полями и движением планет. При скоростях, доступных кораблям сколопендеров, эти факторы не имеют значения, если не подлетать слишком близко к планетам. Мне всего-то был нужен порядок величины.
Жаль, что нет логарифмической линейки. Папа говорил, что тот, кто не умеет ей пользоваться, не должен допускаться до выборов, как неграмотный. У меня прелесть, а не линейка - K&E 20" Log-log Duplex Decitrig. Двадцатидюймовая, дуплексная, с тригонометрией от углов в радианах. Папа осчастливил меня ей после того, как я освоил десятидюймовую, где все углы в градусах. Целую неделю пришлось сидеть на одной картошке, но папа заявил, что предметы роскоши должны стоять в бюджете на первом месте. Я знал, где сейчас эта линейка. Дома, на моём столе.
Ничего страшного. У меня есть цифры, формула, карандаш и бумага.
Прикинем. Жирный сказал "Плутон", "пять дней" и "восемь g".
Задача из двух частей. Половина времени (и половина дистанции) на разгон, потом разворот и вторую часть полёта - торможение. Полное расстояние использовать нельзя, потому что время возводится в квадрат - функция параболическая. В какой же конфигурации Плутон? В противостоянии? В соединении? В стоянии? Плутон в телескоп не видно, кто помнит, в каком он месте эклиптики? Ну, ладно, среднее расстояние 30 А. Е. - будем танцевать от него. Половина этого расстояния в футах 1/2 x 30 x 93,000,000 x 5280. Восемь g: 8 x 32.2 фута./сек./за секунду. - скорость увеличивается на 258 футов в секунду каждую секунду до момента разворота и с такой же скоростью снижается.
Итак, - 1/2 x 30 x 93,000,000 x 5280 = 1/2 x 8 x 32.2 x t2 - и у вас время половины полёта в секундах. Удваиваем. Делим на 2600 чтобы получить часы, на 24, чтобы получить дни. На линейке задачка решается секунд за сорок, проще, чем налоги подсчитать.
У меня ушёл час на вычисления и столько же на проверку. Потом пришлось считать ещё раз, потому что я забыл умножить на 5280, и на одной стороне оказались футы, а на другой - мили. Арифметика такого не любит. Потом я пересчитал ещё раз, потому что уже ни в чём не был уверен. Всё же, логарифмическая линейка - лучшая штука в мире после девушек.
Наконец получился проверенный ответ. Пять с половиной дней. Я на Плутоне.
Примечание редактора: моя версия звучала как My Very Educated Mother Just Served Us Nine Pumpkins. Что до линейки: K&E is Keuffel & Esser, производитель качественных линеек. 20 дюймов - в два раза больше по размеру и точности, чем стандартная линейка. Log-log - расширенная логарифмическая шкала. Duplex - двусторонние шкалы и курсор. Decitrig - десятичные тригонометрические шкалы.
Спасибо Чарльзу Мартину за анализ:

В рассказе Хайнлайна "Небесный лифт", факельный корабль двигался к колонии на Плутоне на ускорении 3.5 g 9 дней и 15 часов. 3.5 g это примерно 35 м/с2 и 9д15ч - 831,600 секунд. 35 м/с2 * 831,600 с = 29,100,000 м/с общего deltaV.
Предположим соотношение масс 4. У большинства кораблей Хайнлайна там использовалось 3, но 4 сойдёт для спасательной операции.
Ve = Δv / ln[R] так что 29,100,000 / 1.39 = 21,000,000 м/с скорости истечения или семь процентов скорости света.
Взгляд на таблицу двигателей показывает, что это уступает лишь лучевому двигателю на антиматерии и вдвое превышает максимум инерциальной ядерной реакции. Если корабль Хайнлайна способен выдать Ve в десять процентов скорости света, ему подойдёт и соотношение масс 3.
В "небесном лифте" и "Двойной Звезде" экипаж проводил дни в режиме большого ускорения в чём-то вроде водяных постелей. (они же "масловыжималка"). В книге "Мошка в зенице господней" Ларри Нивена и Джерри Пурнелла капитанское кресло имело встроенный туалет для периодов долгого ускорения на многократной силе тяжести. Несколько моторизованных кресел использовались аварийными и техническими командами. Такие же моторизованные кресла поминал Джо Холдеман в своей "Бесконечной войне".
Из Мошка в зенице господней Ларри Нивена и Джерри Пурнелла
Вместо этого он вызвал Бари.
Бари лежал в противоперегрузочной ванне, поверхность жидкости в которой покрывала тонкая эластичная пленка Милара. Над вогнутой поверхностью торчало только его лицо и руки. Лицо выглядело очень старым, показывая почти истинный его возраст.
...- Да, конечно, я не имел в виду именно вас. Просто мне хотелось получить информацию о нашем движении. В моем возрасте лучше не вылезать из этой ванны на протяжении всего путешествия. Сколько еще у нас будет четыре g?
- Сто двадцать пять часов. Впрочем, уже сто двадцать четыре.
. . .Он вызвал каюту Сэлли. Она выглядела так, словно не спала неделю или улыбалась целый год.
- Хэлло, Сэлли, - сказал Блейн. - Не жалеете, что остались?
- Я же говорила вам, что могу делать все, что можете вы, - спокойно ответила Сэлли. Она ухватилась руками за стул и встала, вытянув руки вперед, чтобы доказать свои слова.
- Будьте осторожны, - сказал Блейн, стараясь, чтобы голос его звучал ровно, - не делайте резких движений и держите колени прямо. Садясь, вы можете сломать себе спину. Оставайтесь в таком положении и вытяните руки назад. Потом возьмитесь за оба подлокотника, прежде чем попробовать согнуть талию.
Она не поверила, что это так опасно, но лишь до тех пор, пока не попыталась сесть. При этом мышцы ее рук свела судорога, в глазах плеснулась паника, и она села слишком резко, как если бы гравитация "Мак-Артура" всосала ее вниз.
- У вас все в порядке?
- Да, - ответила она, - кроме гордости.
- Вот и оставайтесь в кресле, черт возьми! Разве я стою сейчас? Нет. И вы не смейте!
- Хорошо, - она повертела головой из стороны в сторону. Та явно кружилась от сотрясения.
(Перевод с английского: Олег Колесников)
Из книги Двойная Звезда Роберта Хайнлайна, 1956
Меня ухватили за руку и протащили в отсек по узкому проходу. У стены я увидел две "масловыжималки" - похожие на ванны гидравлические баки, используемые для компенсации высокого ускорения факельных кораблей. Я никогда не видел их вживую, но у нас были убедительные муляжи в постановке космического опуса "Земные Рейдеры".
Над компенсаторными баками висела табличка: ВНИМАНИЕ!!! Запрещается перемещаться при более чем трёхкратном ускорении без компенсаторного костюма. Согласно приказу... я не успел дочитать до конца, потому что меня бросили в одну из масловыжималок. Дак и остальные спешно крепили меня, когда прозвучал сигнал. Он продолжался несколько секунд, а затем прозвучал голос: Внимание! Двукратная перегрузка! Три минуты! Сирена зазвучала снова.
...
Я посмотрел на него и спросил: Как ты умудрился встать? Часть моего мозга, профессионал, что всегда наготове, зафиксировала, как он стоит и поместила в папку с надписью "поза человека при двукратной перегрузке"
Он усмехнулся: "Ничего особенного. Это корсет"
"Хммммпф!"
"Ты тоже можешь встать, если хочешь. Обычно мы не поощряем такое поведение пассажиров при разгоне более чем на полуторной перегрузке - слишком велик риск, что какой-нибудь дурак свалится и сломает ногу. Но я однажды видел, как один реально крутой тяжелоатлет встал и выбрался из пресса на пятикратной перегрузке - но после этого ни к чему больше не годился. А двукратная перегрузка - сущая ерунда. Всё равно, что тащить на закорках ещё одного себя.
...
Назад она не вернулась. Вскоре дверь отворилась, пропустив в каюту человека, находившегося внутри некоего сооружения, наподобие детского стульчика на колесах. - Как мы себя чувствуем? - пробасил он. Выглядел вошедший лет на шестьдесят; был малость полноват, а в обращении несколько ироничен. В диплом его я не заглядывал, но держался он точь-в-точь как врач перед пациентом.
- Неплохо, а вы, сэр?
- Не жалуюсь. То есть, ни на что, кроме ускорения, - добавил он, бросив взгляд на свою каталку, - он был буквально вплетен в нее. - Что вы скажете о моем колесном корсете? Возможно, несколько не по моде, однако в моем возрасте не следует в погоне за модой перегружать сердце.
...
Когда началось торможение, мы получили обещанный Дэком отдых при нормальном притяжении. В невесомости мы не провели ни минуты: вместо того, чтобы выключить двигатели - чего космачи очень не любят, - команда проделала, по словам Дэка, "косой поворот на 180 градусов". Двигатели при этом работали на полную катушку, и маневр сей довольно удачно обманывал ваш вестибулярный аппарат. Не помню, как этот эффект называется. То ли Кориолана, то ли Кориолиса.
Вообще я мало знаю о космических кораблях. Те, что могут стартовать прямо с планеты, космачи презрительно зовут "самоварами" - за густую струю пара или водорода из сопел. Однако они - самые настоящие ракеты, и двигатели их тоже работают на ядерном топливе - в смысле, котел им подогревают, или еще что. Хотя космачи их за корабли не считают. Планетолеты же, вроде "Тома Пейна" замечательны, как мне объяснили, тем, что работают на каком-то Е, равном мс-квадрат, а может, М, равном ес-квадрат... Знаете, наверное: то самое, которое Эйнштейн изобрел.
...
Луна полностью лишена атмосферы, поэтому планетолеты могут садиться прямо на поверхность. Однако "Том Пейн", казалось, обречен был ни на минуту не покидать Пространство, обслуживаясь только на орбитальных станциях. Посадить его можно было лишь на опоры - "в колыбель", как говорят космачи. Когда Дэк ухитрился проделать это, я спал - проспав такое редкое зрелище! Я слыхал, куда легче поймать яйцо тарелкой, не разбив его; Дэк же был одним из полдюжины пилотов, идущих и не на такой риск.